gRain: genetics example

gRain is an R package for "probability propagation in graphical independence networks, also known as probabilistic expert systems (which includes Bayesian networks as a special case)". This package caught my attention because some genetic models can be seen as graphical models, which is a broader class of models encompassing Bayesian networks or sometimes also called Directed Acyclic graphs (DAGs).

A very simple example of DAG in genetics is to draw a pedigree of a small family (say father, mother, and child) with three nodes representing their genotype (g01, g02, and g03). Nodes are logically connected, father to child (g01 --> g03) and mother to child (g02 --> g03). Assume we observe some phenotype condition in a child and if we postulate that this phenotype is affected by genotype, we draw another connection between genotype and phenotype of a child (g03 --> p03).

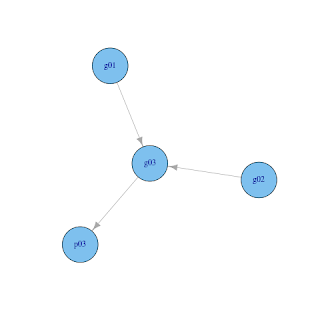
This kind of problems/models are often postulated and one might want to do some queries about the genotype of individuals given some data (observed phenotype and/or genotype). Can we do this in R? Yes, this can be neatly done with the gRain package.

Before digging into the code we need to pause to see how can we describe the above model? If you have read at least some parts of Wikipedia links provided above than it should be straightforward to understand the following factorization of this simple model: p(g01, g02, g03, p03) = p(g01) p(g02) p(g03|g01, g02) p(p03|g03). The terms p(g01) and p(g02) are often called prior distributions (probabilities) of genotypes in some population. Term p(g03|g01, g02) describes probability of genotype in child (g03) given that we know the genotype of parents (g01 and g02). This is actually very simple part and often referred as transmission probability If there are only two alleles (gene variants) in population (A and a) and father is AA and mother is AA then child must also be AA or p(g03|g01=AA, g02=AA) = (1, 0, 0), where number show probability for genotype AA, Aa, and aa. The last term p(p03|g03) is often called penetrance function and tells us the conditional probability of some phenotype given the genotype data. Let us assume that we are interested in some binary condition, which is under very very large influence of genotype, but expressed primarily in individuals with genotype aa. Bellow is R code for specifying such a model with some additional details skipped in the text.

## Set of genotype values
geno <- c("AA", "Aa", "aa")

## Prior allele frequencies in (founder) population
PrA <- 2/3
(Pra <- 1 - PrA)

## Prior genotype frequencies in (founder) population - according to Hardy-Weinberg's law
(gP <- c(PrA*PrA, 2*PrA*Pra, Pra*Pra))

## Genotype frequencies in children given the genotype of parents - according to Mendel's law 
gM_AA_AA <- c(  1,   0,   0)
gM_AA_Aa <- c(1/2, 1/2,   0)
gM_AA_aa <- c(  0,   1,   0)

gM_Aa_AA <- c(1/2, 1/2,   0)
gM_Aa_Aa <- c(1/4, 1/2, 1/4)
gM_Aa_aa <- c(  0, 1/2, 1/2)

gM_aa_AA <- c(  0,   1,   0)
gM_aa_Aa <- c(  0, 1/2, 1/2)
gM_aa_aa <- c(  0,   0,   1)

gM <- c(gM_AA_AA, gM_AA_Aa, gM_AA_aa,
gM_Aa_AA, gM_Aa_Aa, gM_Aa_aa,
gM_aa_AA, gM_aa_Aa, gM_aa_aa)

## Set of phenotype values
phen <- c("OK", "NOK")

## Error rate (= 1 - penetrance)
e <- 0.01

## Phenotype frequencies in individual given the genotype of individual - penetrance
##      OK  NOK
p <- c(1-e, 0+e, ## AA
1-e, 0+e, ## Aa
0+e, 1-e) ## aa

## Graph - joint distribution
g01 <- cptable(~g01,             values=gP, levels=geno)
g02 <- cptable(~g02,             values=gP, levels=geno)
g03 <- cptable(~g03 + g01 + g02, values=gM, levels=geno)
p03 <- cptable(~p03 + g03,       values=p,  levels=phen)

## Compile model
plist <- compileCPT(list(g01, g02, g03, p03))
g <- grain(plist)
summary(g)

## Plot the model
iplot(g)

Now if we want to query our model without any observed data, but just using parameter values for this population we use the following code:

## Query model given parameter values (=prior)
querygrain(g, nodes=c("g01", "g02", "g03"))

which returns probabilities shown bellow. Not really interesting, but we should not expect much as we did not observe any data. Genotype probabilities are equal for all individuals and they are completely defined by population parameters.

$g01
g01
   AA        Aa        aa
0.4444444 0.4444444 0.1111111

$g02
g02
   AA        Aa        aa
0.4444444 0.4444444 0.1111111

$g03
g03
   AA        Aa        aa
0.4444444 0.4444444 0.1111111

Now we can add some data and repeat the query again.

g <- setFinding(g, nodes="p03", states="NOK")
summary(g)
## Query model given parameter values (=prior) + some data
querygrain(g, nodes=c("g01", "g02", "g03"))

Results show probability of such finding (that phenotype condition was observed) given the defined model and parameters. Probability is not really high. Further on we get updated genotype probabilities and we can see the change due to introduction of phenotype information. Now we can claim with high confidence that child has genotype aa, while there is still quite some ambiguity about genotypes of parents as there are several possible combinations of parent genotypes that would give aa genotype in child (Aa x Aa, Aa x aa, aa x Aa, and aa x aa).

Independence network: Compiled: TRUE Propagated: TRUE
Nodes : chr [1:4] "g01" "g02" "g03" "p03"
Number of cliques:                 2
Maximal clique size:               3
Maximal state space in cliques:   27
Finding:
   variable state
[1,] p03      NOK
Pr(Finding)= 0.1188889

$g01
g01
      AA         Aa         aa
0.03738318 0.64797508 0.31464174

$g02
g02
      AA         Aa         aa
0.03738318 0.64797508 0.31464174

$g03
g03
      AA         Aa         aa
0.03738318 0.03738318 0.92523364

This is all for the purpose of this blog post, but it should be clear that it is very easy to extend our model either with model individuals (just defined them with cptable and compile in joint model) or with other stuff (more alleles leads to more genotypes, other penetrance function, sex-linked genes, ...).